
Aula 52 - Operações com números inteiros
02/06/2015
Exemplos e resolução de problemas com situações do dia a dia que envolvem operações com números inteiros; números opostos ou simétricos (definição e identificação); multiplicação e divisão: números positivos e negativos; definição de potenciação; exercício com a correção na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 51 - Fatoração de polinômios
02/06/2015
Conceito de fatoração; apresentação e resolução de situações exemplares que envolvem os três casos especiais de fatoração de polinômios: 1º caso (fator comum), 2º caso (agrupamento) e 3º caso (diferença de dois quadrados); questão com a correção na videoaula seguinte.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 50 - Análise e interpretação de gráficos da função quadrática
02/06/2015
Interpretação de gráficos de funções quadráticas envolvidos em um problema; identificação dos elementos do gráfico (zeros da função, ponto de vértice, crescimento e decrescimento); análise dos sinais da função; proposição de exercícios de fixação a serem corrigidos na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 49 - Resolvendo problemas com função quadrática
02/06/2015
Correção de exercício; identificação, interpretação e análise de problemas que envolvem a função quadrática; análise dos elementos que constituem o domínio das funções trabalhadas; problemas com a correção na videoaula seguinte.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 48 - Máximos e mínimos: o ponto de vértice
02/06/2015
Correção de exercício; cálculo do ponto vértice de uma função quadrática (parábola), por meio da análise de gráficos exemplares (com concavidades diferentes) – identificação dos pontos (máximo e mínimo) e relação com a concavidade; identificação do vértice da parábola; identificação da coordenada de x do vértice como ponto médio das coordenadas dos zeros da função (conceito de simetria da parábola); cálculo das fórmulas do xv, yv e suas aplicações; exercício de fixação a ser corrigido na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 47 - Construção da parábola
02/06/2015
Elaboração de uma tabela de valores de x e de f(x) de cada função e representação dos pontos obtidos na tabela no plano cartesiano; identificação do padrão parabólico dos pontos de uma função quadrática; determinação dos pontos importantes para a construção de um gráfico de uma função quadrática; apresentação de algumas aplicações das parábolas no dia a dia (antena parabólica, holofote, etc.); exercício de fixação a ser corrigido na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 46 - Os zeros da função quadrática
02/06/2015
Cálculo de alguns valores da função f – valor numérico; verificação da existência de um valor de x que faz com que a função y seja zero (zero da função); cálculo de f(x) = 0 (resolução de uma equação do 2º grau); verificação de funções que não possuem zeros da função e outras que possuem apenas um (estudo do discriminante de uma equação do 2º grau); gráficos de funções quadráticas com enfoque nos zeros da função. Exercício a ser corrigido na próxima aula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 45 - A função do 2º grau
02/06/2015
Conceito de função quadrática (função do 2º grau) como uma função formada a partir de um polinômio do 2º grau do tipo ax2 + bx + c; reconhecimento dos coeficientes a, b e c de uma função quadrática; análise do coeficiente a, como responsável pela concavidade da parábola; problema com a correção na videoaula seguinte.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 44 - Interpretação e análise de gráficos de função afim
02/06/2015
Correção de exercícios; análise de gráfico de uma função polinomial de 1º grau (função afim) – características (crescimento, decrescimento, zero da função, estudo dos sinais, etc.) e identificação de informações complementares; problema envolvendo diferentes funções e gráficos com interpretação dos coeficientes angular e linear da função e seus efeitos no gráfico de uma função afim; proposição de desafio com resolução na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 43 - Construção de gráficos de funções afim
02/06/2015
Construção do gráfico de uma função afim (1º grau); análise das coordenadas (x, y) de um ponto como representação geométrica da relação do valor de x com f(x); construção de uma tabela de valores de x e de f(x) de cada função; representar os pontos obtidos no plano cartesiano; identificar o padrão retilíneo dos pontos e construir a reta que representa a função afim; exercício a ser corrigido na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 42 - Resolução de problemas envolvendo função afim
02/06/2015
Correção de exercícios; identificação, num problema, da função afim (y = ax + b); interpretação de uma função afim dentro de um problema; análise dos elementos que constituem o domínio das funções trabalhadas; questão com resolução na videoaula seguinte.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 41 - O zero da função afim
02/06/2015
Cálculo de alguns valores da função f – valor numérico; verificação da existência de um valor de x que faz com que a função y seja zero; cálculo de f(x) = 0 e identificação do zero da função como coordenada (x = 0) do gráfico no plano cartesiano; proposição de exercícios a serem corrigidos na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 40 - A função afim
02/06/2015
Correção de exercícios; identificação da expressão y = ax + b como uma função do 1º grau; como reconhecer a e b como coeficientes angular e linear de uma função afim; problema com a correção na videoaula seguinte.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 39 - Relações e funções
02/06/2015
Definição e características de relações entre conjuntos numéricos ou não; exercício de fixação a ser corrigido na próxima videoaula.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 38 - Números reais na reta numérica
02/06/2015
Reta numérica: definição, usos e aplicações na vida cotidiana; construção de uma reta numérica com números reais e racionais; resolução de problemas.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 37 - Pontos no plano cartesiano
02/06/2015
Identificação e marcação de pontos num plano cartesiano; coordenadas e quadrantes de um plano cartesiano; resolução de problemas.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 36 - Valor numérico de uma expressão algébrica
02/06/2015
Definição de expressões numéricas; resolução de problemas.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 35 - Noções de juros compostos
02/06/2015
Definição de juros compostos e sua principal utilização (mercado financeiro); demonstração do cálculo em situações que envolvem juros compostos; resolução de problemas.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 34 - Noções de juros simples
02/06/2015
Nomenclaturas utilizadas em situações que envolvem juros (juro, capital, taxa de juros e montante); definição de juros simples e exemplos de sua utilização no dia a dia; resolução de problemas.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 33 - Problemas com porcentagem
02/06/2015
Conceito de porcentagem; uso e cálculo de porcentagem em situações cotidianas; resolução de problemas.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
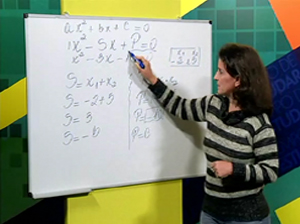
Aula 32 – Composição da equação do 2º grau com raízes
02/06/2015
Confira o exercício da aula 21 e aprenda a montar uma equação de 2º grau a partir do resultado, ou seja, a partir do valor de suas raízes, sejam elas números positivos, negativos ou fracionários. Não deixe de fazer a tarefa proposta!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 31 – Soma e produto das raízes da equação do 2º grau
02/06/2015
Corrija a tarefa da aula 20 e veja como é fácil calcular a soma e o produto das raízes de uma equação de 2º grau, usando apenas as relações de Girard (sem precisar aplicar a fórmula de Bhaskara). Fixe o conteúdo, resolvendo o exercício proposto.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 30 – O discriminante da equação do 2º grau
02/06/2015
Depois de conferir a tarefa da aula 29, amplie seu conhecimento sobre o △ (delta) da fórmula de Bhaskara. Quais são as características das equações que têm △ positivo, ou negativo, ou igual a zero? Não se esqueça de fazer o exercício para fixar o assunto.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 29 – Equações do 2º grau: fórmula de Bhaskara
02/06/2015
Após conferir o exercício da aula 28, veja uma explicação com o passo a passo da aplicação da fórmula de Bhaskara em equações de 2º grau. Faça a tarefa para ficar fera na matéria!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 28 – Equações incompletas do 2º grau – 2ª parte
02/06/2015
Corrija o exercício da aula 27 e aprenda a resolver as equações incompletas de 2º grau do tipo ax² + c. Entenda por que, quando admitirem raízes reais, elas sempre serão opostas. Não deixe de fazer os exercícios de fixação!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 27 – Equações incompletas do 2º grau – 1ª parte
02/06/2015
Depois de corrigir a tarefa da aula 26, aprenda a resolver as equações incompletas de 2º grau do tipo ax² + bx. Entenda por que elas têm duas raízes, sendo uma delas sempre zero. Não deixe de fazer os exercícios de fixação!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
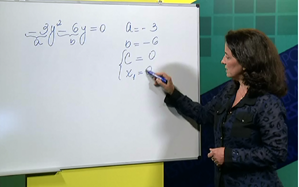
Aula 26 – Raízes de uma equação do 2º grau
02/06/2015
Após a correção do exercício da aula 25, saiba como determinar as raízes das equações de 2º grau. Faça o exercício para garantir a assimilação do conteúdo.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 25 – Reconhecendo uma equação do 2º grau
02/06/2015
Veja se acertou a tarefa da aula 24 e entenda os conceitos que definem uma equação de 2º grau, seja ela completa ou incompleta. Fixe o assunto, resolvendo o exercício sugerido.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
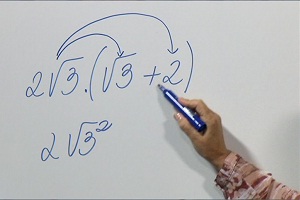
Aula 24 – Potenciação com radicais e racionalização de denominadores
02/06/2015
Corrija o exercício da aula 23 e veja como calcular as raízes elevadas a alguma potência (com fator externo ou não), aplicando a regra do produto notável ou a propriedade distributiva da multiplicação. Na mesma aula, racionalização de frações com raízes no denominador. Garanta a fixação do conteúdo, resolvendo o exercício proposto.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
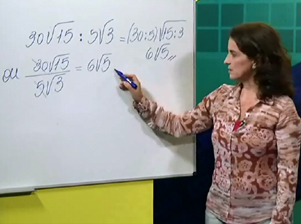
Aula 23 – Multiplicação e divisão com radicais
02/06/2015
Depois de conferir o exercício da aula 22, aprenda a multiplicar e a dividir os radicais semelhantes e diferentes (com fatores externos ou não), aplicando as regras do produto notável e as propriedades da multiplicação e da divisão. Tenha certeza de que assimilou o conteúdo, resolvendo a tarefa sugerida.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 22 – Adição algébrica com radicais
02/06/2015
Correção do exercício da aula 21 e explicações sobre como somar e diminuir radicais semelhantes (com fatores externos ou não) e como resolver expressões com radicais diferentes. Para garantir que aprendeu o assunto, faça as tarefas propostas!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 21 – Operações com radicais
02/06/2015
Após a correção da tarefa da aula 20, aprenda a calcular o valor aproximado das raízes imperfeitas. Não deixe de fazer os exercícios de fixação!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 20 – Simplificação de radicais
02/06/2015
Além da correção da tarefa da aula 19, você acompanha exercícios de simplificação de radicais que aplicam as regras de suas propriedades em raízes perfeitas, imperfeitas e com fatores externos. Também aprende a fazer o caminho inverso, ou seja, a calcular o valor do radical que deu origem ao termo simplificado. Para garantir o aprendizado, faça os exercícios sugeridos!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 19 – Propriedades dos radicais
02/06/2015
Corrija a tarefa da aula 18 e conheça as propriedades dos radicais. Elas são fundamentais para fazer equivalências entre as raízes e facilitar a resolução dos cálculos. Faça os exercícios e fixe os conteúdos aprendidos!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 18 – Radicais: simplificando
02/06/2015
Depois de corrigir as tarefas da aula 17, recorde uma operação fundamental para a simplificação dos radicais: a fatoração. Aprenda, também, que há mais de um caminho para calcular o resultado de uma raiz, desde que se observe a relação entre índice e expoente. Confira se você entendeu mesmo o conteúdo, fazendo os exercícios propostos.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 17 – Radicais
02/06/2015
Veja se acertou a tarefa da aula 16 e fique por dentro dos termos da radiciação: índice, radical, radicando e raiz. Entenda, também, qual é a relação entre índice e expoente e aprenda a calcular as raízes de números inteiros e fracionários, positivos e negativos. Depois, faça as tarefas para fixar o assunto.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
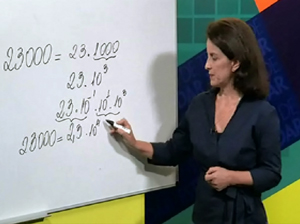
Aula 16 – Notação científica
02/06/2015
Correção da tarefa da aula 15, para depois aprender a representar, de forma simples, os números muito grandes ou muito pequenos (cheios de dígitos depois da vírgula). Por fim, exercícios para ficar fera no assunto!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 15 – Potência de base dez
02/06/2015
Corrija os exercícios da aula 14 e aprenda tudo sobre potências de base 10. Como fazer quando elas têm expoente negativo (ou positivo)? Como expressá-las por meio de um número decimal? Como multiplicá-las, dividi-las e simplificá-las? Garanta a aprendizagem, fazendo os exercícios de fixação do assunto!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
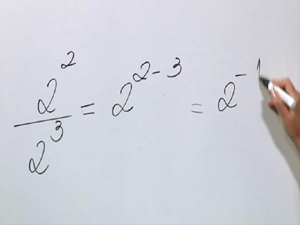
Aula 14 – Propriedades das potências: expoente zero, um e negativo
02/06/2015
Confira a explicação e a resolução do exercício da aula 13 e veja como é fácil calcular potências com expoentes negativo, zero e um. Não deixe de resolver os exercícios propostos no fim da aula!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
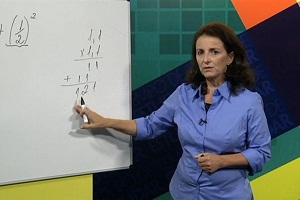
Aula 13 – Propriedades das potências
02/06/2015
Além de conferir a resolução e a explicação dos exercícios da aula 12, você aprende a multiplicar e a dividir potências de mesma base. E entende como é fácil calcular a potência de uma potência e a potência de um produto. Para não esquecer a lição, faça a lista de tarefas!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 12 – Potência de base racional
02/06/2015
Aqui você encontra a resposta e a explicação do exercício de fixação da aula 11 e aprende a calcular as potências de números fracionários e decimais (negativos e positivos). No final, questões para resolver.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
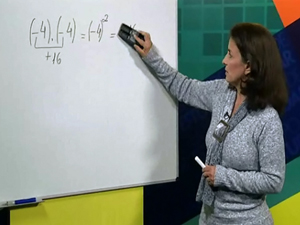
Aula 11 – Potências
02/06/2015
Nessa aula, você entende o que é base e expoente; aprende a calcular as potências de bases positiva e negativa; e a resolver, rapidamente, as potências de base 10. Também tem exercício para fixar o assunto!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 10 – Círculo e circunferência
02/06/2015
Depois da correção do exercício da aula 9, veja a diferença entre essas duas figuras geométricas. Depois, como se calcula o comprimento da circunferência e a área do círculo.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
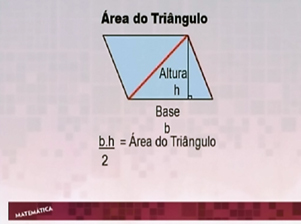
Aula 8 – Áreas de figuras planas: triângulo
02/06/2015
Confira o exercício da aula 7, aprenda a calcular a área dos triângulos – com atenção ao caso particular do triângulo retângulo – e faça a tarefa proposta!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
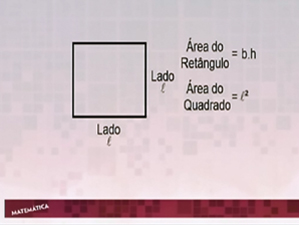
Aula 7 – Áreas de figuras planas: retângulo, quadrado e paralelogramo
02/06/2015
Correção da tarefa da aula 6 e apresentação do m² e do cm² para você ter noção do tamanho dessas medidas. Depois, o cálculo das áreas do retângulo, do quadrado e do paralelogramo. O exercício de fixação do assunto apresenta situações da vida prática.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 6 – Ângulos notáveis
02/06/2015
Depois de conferir a tarefa da aula 5, veja a explicação sobre os ângulos notáveis (30°, 45° e 60°) presentes no triângulo equilátero e no quadrado, e suas relações com o triânguloretângulo. Por fim, exercícios de fixação do assunto!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
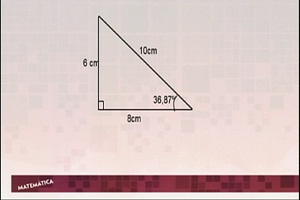
Aula 5 – Relações trigonométricas no triângulo retângulo
02/06/2015
Após a correção dos exercícios da aula 4 e uma explicação sobre as relações entre as medidas dos catetos e da hipotenusa, você aprenderá a calcular o seno, o cosseno e a tangente dos triângulos retângulos. Garanta a aprendizagem, fazendo a tarefa proposta!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
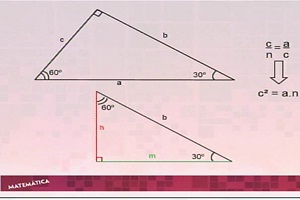
Aula 4 – Relações métricas do triângulo retângulo – Teorema de Pitágoras
02/06/2015
Correção da tarefa da aula 3 e duas demonstrações para entender por que, em triângulos retângulos, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos, ou seja, por que a² = b² + c². Depois disso, a aplicação do teorema em situações da vida prática e um exercício para fixar a matéria.
Fique Esperto - Tempo de Estudar - Matemática - 9º ano
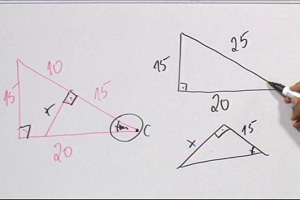
Aula 3 – Relações métricas do triângulo retângulo
02/06/2015
Além de conferir a resolução da tarefa da aula 2, você aprende a calcular segmentos desconhecidos de um triângulo retângulo, a partir do conceito de projeção ortogonal e suas relações de correspondência. Para não esquecer a lição, faça os exercícios!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 2 – Semelhança: semelhança de triângulos
02/06/2015
Primeiro, você confere a resposta dos exercícios de fixação da aula 1. Depois, aprende a calcular segmentos desconhecidos de um triângulo, a partir do conceito de razão de semelhança e da identificação dos tipos de semelhança. Por fim, questões para exercitar o conteúdo!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano

Aula 1 – Teorema de Tales
02/06/2015
Após revisar os conceitos de unidade de medida, razão e proporção, você entenderá quais são as relações matemáticas estabelecidas entre as retas paralelas e suas diagonais. Para ter certeza de que aprendeu o assunto, faça os exercícios propostos!
Fique Esperto - Tempo de Estudar - Matemática - 9º ano














